KarNaugh MaAP

Contoh peta Karnaugh Peta Karnaugh (K-peta untuk pendek), 1953 perbaikan Maurice Karnaugh tentang diagram 1952 Veitch Edward Veitch, adalah sebuah metode untuk menyederhanakan ekspresi aljabar Boolean. Peta Karnaugh mengurangi kebutuhan untuk perhitungan luas dengan mengambil keuntungan dari kemampuan pengenalan pola manusia ', yang memungkinkan identifikasi cepat dan penghapusan kondisi ras potensial. Dalam peta Karnaugh variabel boolean ditransfer (umumnya dari tabel kebenaran) dan memerintahkan sesuai dengan prinsip-prinsip kode Gray di mana hanya satu variabel perubahan di antara kotak yang berdekatan. Setelah tabel dihasilkan dan kemungkinan output ditranskripsi, data diatur ke dalam kelompok terbesar yang mungkin mengandung sel-sel 2n (n = 0,1,2,3 ...)[ 1] dan minterm yang dihasilkan melalui hukum aksioma aljabar boolean.










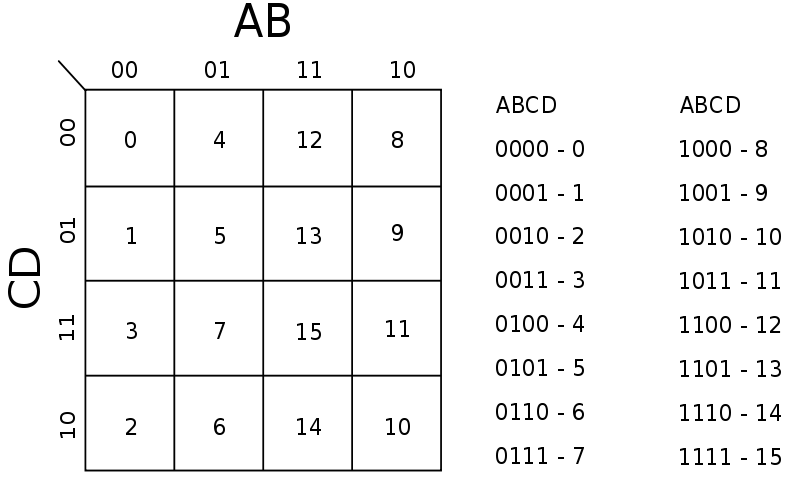
K-peta konstruksi.
Variabel input dapat dikombinasikan dalam 16 cara yang berbeda, sehingga petaKarnaugh memiliki 16 posisi, dan karena itu diatur dalam 4 × 4 grid.
Angka biner dalam peta merupakan keluaran fungsi untuk setiap kombinasi input tertentu.Jadi 0 adalah ditulis di sudut paling kiri atas dari peta karena ƒ = 0 bila A = 0, B = 0, C =0, D = 0. Demikian pula kita tandai sudut kanan bawah sebagai 1 karena A = 1, B = 0, C= 1, D = 0 memberikan ƒ = 1. Perhatikan bahwa nilai-nilai yang diperintahkan dalam kodeGray, sehingga tepat satu variabel perubahan antara sepasang sel yang berdekatan.
Setelah peta Karnaugh telah dibangun tugas berikutnya adalah untuk menemukan istilahminimal untuk digunakan dalam ekspresi akhir. Istilah-istilah ini ditemukan oleh kelompokmengelilingi 1s dalam peta. Kelompok-kelompok harus persegi panjang dan harusmemiliki luas yang merupakan kekuatan dua (yaitu 1, 2, 4, 8 ...). Persegi panjang harusseluas mungkin tanpa mengandung 0s apapun. Pengelompokan optimal dalam peta iniditandai oleh, garis hijau merah dan biru. Perhatikan bahwa kelompok mungkin tumpang tindih. Dalam contoh ini, kelompok merah dan hijau tumpang tindih. Kelompok merah adalah persegi 2 × 2, kelompok hijau adalah 4 × 1 persegi panjang, dan daerah tumpang tindih ditunjukkan dalam coklat.
Grid toroidally terhubung, yang berarti bahwa kelompok-kelompok persegi panjang bisa membungkus di sekitar tepi, sehingga adalah istilah yang valid, meskipun bukan bagian dari minimal set-ini mencakup Minterms 8, 10, 12, dan 14.
Mungkin yang paling sulit-untuk-memvisualisasikan membungkus-sekitar istilah yang mencakup empat sudut-ini mencakup minterm 0, 2, 8, 10









http://en.wikipedia.org/wiki/Karnaugh_map